| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- OculusMotionVectorPass
- 3d
- 작업 집합
- 프로그래밍 기초
- ColorGradingLutPass
- URP로 변경
- 개인 바이트
- Specular
- AppSW
- Cell Shader
- Three(Two) Tone Shading
- 가상 바이트
- ASW(Application SpaceWarp)
- Cell Look
- URP
- 게임 수학
- 메모리 누수
- VR
- Rim Light
- Virtual Byte
- Private Bytes
- C언어
- Cartoon Rendering
- 벡터
- Windows Build
- Toon Shader
- working set
- Today
- Total
WinCNT
삼각비와 삼각 함수 본문
삼각법(Trigonometry)
(유클리드 기하학에서) 삼각형의 변과 각 사이의 관계에 따른
여러 가지 기하학적 도형을 연구하는 수학의 한 분과이다
특히 삼각법에서 직각삼각형의 빗변은 항상 밑변, 높이와 일정한 비율을 유지한다는 것을
보여주는 것이 바로 삼각비(trigonometric ratio)이다
삼각법은 고대 이집트에서 피라미드를 건설할 때부터 사용된 것으로 여겨지며
측지학과 측량, 천체역학, 항법과 같은 분야에서 널리 사용되었다
고대 사람들은 삼각함수 표를 들고 다녔음
3D 게임 프로그래밍에서 사인과 코사인(서로 직교 관계)이 많이 사용되며
노멀 맵핑이란 기법에는 탄젠트 스페이스라는 용어도 등장한다
그런데 탄젠트란 단어를 빌려왔을 뿐 직접적인 연관은 없는 것처럼 보인다...
삼각함수(Trigonometric Functions)
삼각비와는 다르다 삼각비와는!!
삼각비를 확장한 것이 바로 삼각함수이며, 말 그대로 각의 크기를 삼각비로 나타내는 함수이다
삼각함수의 정의는 2가지가 있다
1. 반지름 r인 원의 좌표계(기하학적인 정의)
2. 테일러 급수 전개를 사용한 정의(해석학적인 정의)
각도법과 호도법
각도법은 일반적으로 사용하는 원주를 360으로 나눈 것을 1도로 정한 것이다(단위 : 도, degree)

호도법은 호(arc)의 길이로 각도를 나타내는 방법이다(단위 : 라디안, Radian)

실제로 코딩에서 사용하는 것은 호도법(!)이다

각도법과 호도법은 서로 변환할 수 있다

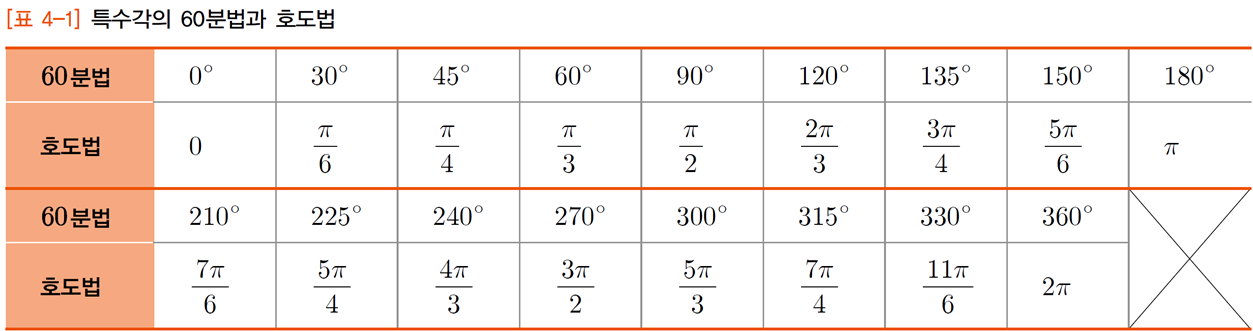
유니티 같은 에디터에서, 기획자들은 실제 각도를 넣지만 내부적으로는 라디안으로 치환해줘야 한다

삼각함수의 정의
반지름이 1인 원이 있다면 cos은 원의 x좌표, sin은 원의 y좌표이다
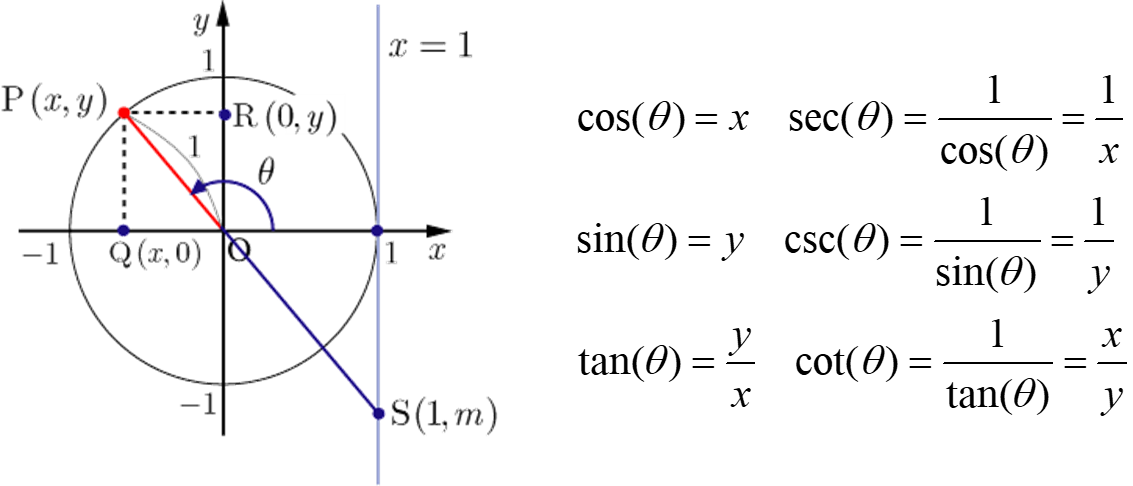
3D 그래픽스에서는 많이 쓸 일은 없지만(그래도 가끔은 쓰임) 사인, 코사인, 탄젠트의 역수도 존재한다
코시컨트(영어: cosecant, csc), 시컨트(영어: secant, sec), 코탄젠트(영어: cotangent, cot)
역(삼각)함수

벡터의 내적
벡터를 내적하면 cosθ의 값을 구할 수 있고,
cosθ의 역함수(아크코사인)을 하면 각도를 구할 수 있다
이는 오브젝트의 회전에 주로 사용한다
컬링 노이즈
파도와 같이 주기성을 나타날 때 사인 함수를 많이 쓴다
(사인 함수가 0부터 시작해서 코사인 함수보다 좀 더 자연스러움)
삼각함수의 주기와 진폭
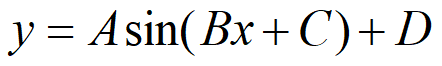
A 진폭(Amplitude) : 진동의 중심으로부터 최대로 움직인 거리
B 주기(Period) : 하나의 완전한 사이클에 걸리는 시간
C 위상변이(phase shift)
D 수직변이(vertical shift)
SSS
'게임 프로그래밍(학습 내용 정리) > 게임 수학' 카테고리의 다른 글
| 변환 파이프라인 (0) | 2022.01.04 |
|---|---|
| 좌표계 (0) | 2021.12.28 |
| 행렬 (0) | 2021.12.21 |
| 수열(Sequence)과 급수(Series) (0) | 2021.10.26 |
| 게임 수학 - 벡터 (0) | 2021.10.12 |




