| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- working set
- C언어
- AppSW
- ASW(Application SpaceWarp)
- Private Bytes
- URP
- URP로 변경
- Three(Two) Tone Shading
- 개인 바이트
- Cell Look
- Virtual Byte
- Rim Light
- Cell Shader
- Windows Build
- 프로그래밍 기초
- 작업 집합
- 벡터
- VR
- 3d
- ColorGradingLutPass
- Specular
- Cartoon Rendering
- OculusMotionVectorPass
- 메모리 누수
- 게임 수학
- 가상 바이트
- Toon Shader
- Today
- Total
WinCNT
게임 수학 - 벡터 본문
벡터와 스칼라
- 스칼라 : 크기에 의해서만 결정되는 양
- 벡터 : 크기와 방향에 의해 결정되는 양(Vertex랑 혼용해서 사용한다!!)
스칼라는 무게나 키와 같이 방향성은 없고 크기에 의해서만 양이 결정되지만
벡터는 크기는 물론 방향에 의해서도 양이 결정됩니다.
벡터는 3차원 공간에서 오브젝트들을 컨트롤하기 위해 많이 사용된다.
벡터의 표현

일반적으로 벡터는 왼쪽과 같이 표현합니다.
- 시점(P) : 벡터가 시작되는 화살표의 꼬리
- 종점(Q) : 벡터의 마지막 부분인 화살표의 머리
- 크기(a) : 방향과 상관없는 화살표의 길이
벡터의 크기
벡터의 크기는 일반적으로 |A|로 표기한다.

벡터 A의 크기를 구하는 공식은 다음과 같다.

이 공식은 피타고라스 정리에 의해 유도 될 수 있습니다.


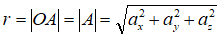
단위 벡터(Unit Vector)
벡터에서는 방향이 특히 중요한 성질이다.애초에 방향이 없으면 그냥 크기일 뿐...
반대로 말하면, 벡터에 대해서 크기의 성분을 배제하고 방향의 성분만 남기는 작업이 중요하고도 할 수 있다.
벡터의 크기를 1로 만들어 크기의 성분을 배제하는 작업을 정규화(normalize)라고 하며,
벡터의 크기가 1, 즉 방향의 성분만 남은 벡터를 단위 벡터(unit vector)라고 한다.
정규화하는 방법은 간단합니다.
벡터의 각 요소들을 벡터의 크기로 나눠주면 되죠.
즉, 수식으로 표현하면 다음과 같습니다.

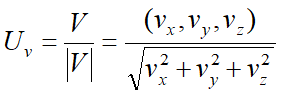
이는 게임 수학에서 정말 많이 사용할 함수가 될 것이라고 합니다...
예를 들어 3D 오브젝트를 비추는 빛의 벡터에 대해서,
단순히 그 값을 크게 하면 빛이 너무 강해서 오브젝트가 하얗게 타버릴(?) 것입니다.
여기서 빛의 벡터를 정규화한다면 빛의 밝기는 유지한 채로 3D 오브젝트에 대한 빛의 방향만 바꿀 수 있게 됩니다.
그럼 다음으로 벡터의 연산에 대해서 하나씩 알아보도록 하겠습니다.
벡터 연산 - 덧셈
벡터의 덧셈은 간단합니다. 각각의 성분을 더해주면 되죠.
수식으로 표현하면 다음과 같습니다.
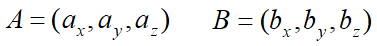
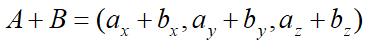
이를 기하학으로 나타내면 다음과 같다.
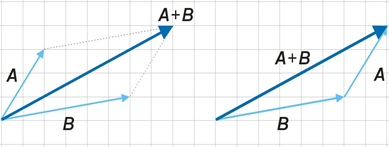
즉, A + B의 값은 B만큼 이동한 뒤에 A만큼 이동한 값과 동일하다는 뜻이 된다.
반대로 A만큼 이동한 뒤에 B만큼 이동해도 동일한 결과가 되는 것을 확인할 수 있다.
(즉, 교환법칙이 성립)
하지만 3D 프로그래밍에서 벡터의 곱셉을 사용하는 경우는 그다지 많지 않다.
벡터 연산 - 스칼라 곱(상수 곱)
벡터의 스칼라 곱도 간단합니다. 이번에는 각각의 성분에 스칼라를 곱하면 됩니다.
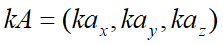
벡터 연산 - 뺄셈
벡터끼리의 뺄셈도 계산 자체는 간단하다.
유도도 스칼라 곱을 이용하면 직관적으로 이해할 수 있다.
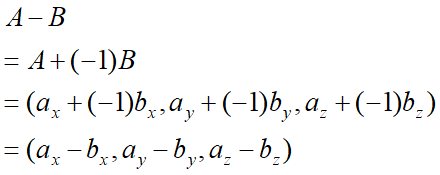
하지만!!!
벡터의 뺄셈은 계산 그 자체보다 기하학적인 의미가 매우 중요!!!
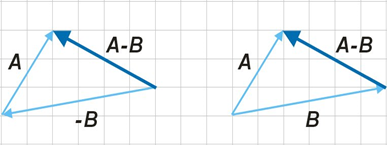
왼쪽의 그림은 벡터의 뺄셈을 기하학적으로 나타낸 것
이 그림을 보면 A - B의 결과가 A의 위치
예시)
A(1, 1, 1), B(3, 3, 3)일 때, B가 내 위치라고 가정하자
A - B = (-2, -2, -2)이므로 정규화를 하면 "대략적"으로 (-1/2, -1/2, -1/2)라는 벡터가 나온다
이 (-1/2, -1/2, -1/2)는 B에서 A를 향하는 방향 벡터이다.
만약 B에서 (-1/2, -1/2, -1/2)를 더하면 B와 A의 직선상의 위에 존재할 것이다.
하지만 B에서 A로 이동하기 위해서 바로 (-1/2, -1/2, -1/2)를 더하면
순간이동을 하는 것처럼 보이기 때문에 (-1/2, -1/2, -1/2) * v(속도)한 값으로 더해주게 된다.
이는 3D 공간에서 매우 중요한 역할을 한다!!!
뺄셈의 연산은!!!! 기하학적인 의미가 더 중요하다
A - B의 경우는 B가 A로 이동하는 효과가 나온다
벡터 연산 -내적(dot product, inner product, scalar product)
A・B = |A||B|cosθ
※실제 cos함수를 구하는 것은 테일러 급수로 구현되어 있다.
여기에 단위 벡터를 이용하면 벡터의 방향 성질만 남길 수도 있다
내적의 용도 - 사잇각
두 개의 벡터를 정규화해서 내적하면 두 개의 벡터의 각도를 구할 수 있다
내적은 곱셈 3번, 덧셈 2번으로 연산비용이 저렴하면서, cosθ의 값(!!!)을 구할 수 있기 때문에 매우 유용하다
(실제로 cosθ의 값을 구하려면 테일러 급수 등의 비싼 연산 비용이 필요하다)
A・B < 0 둔각
A・B = 0 직각
A・B > 0 예각
벡터의 내적으로 많은 것을 나타낼 수 있다
보이는 면을 판단할 때 사잇각이 사용될 수 있다
모든 폴리곤에는 앞면을 나타내는 노말 벡터가 있음
시선(카메라 뷰)와 노말 벡터의 내적의 값이 0보다 크면(즉 둔각이면) 안 보이는 면이고 그릴 필요가 없다
이것이 백 페이스 컬링
내적의 용도 - 확산광 계산
내적을 이용하면 그 지점에서의 밝기 값, 즉 확산광을 구할 수 있다
확산광을 구하기 위해서는 메시 표면의 법선 벡터(Normal Vector)와 광원 벡터(Light Vector)
실제 확산광을 계산할 때 법선 벡터에서 광원 벡터로 나가는 식으로 계산한다
0도일 때 가장 밝고 90일 때 어두워졌다가 270도부터 360도까지 가장 다시 밝아진다(cos함수)
내적의 용도 - 가시성 판단
3D 그래픽스에서 중요한 것은 최대한 예쁘게 그리는 것이 아니라
쓸데 없는 것을 안 그림으로써 퍼포먼스를 높이는 것!!
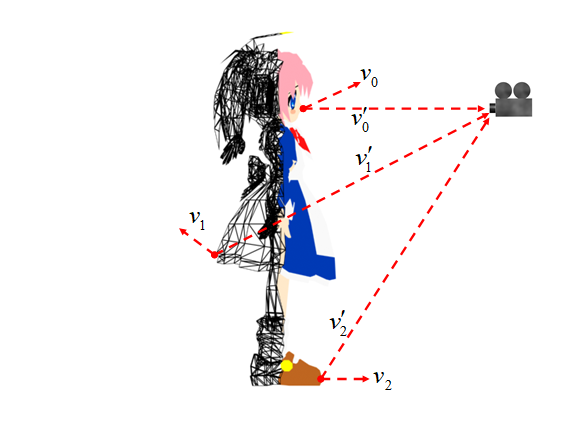
실제 렌더링 화면과 렌더링이 필요 없는 데이터
V0는 노멀 벡터 - 폴리곤의 앞면(수직)인 벡터
모든 폴리곤에는 앞면, 뒷면이 있는데 버텍스를 시계 방향으로 감쌀 때 위를 향하는 것이 노멀 벡터(V0)
(물론 반대도 가능 - 사용자가 임의로 정할 수 있다)
번외1) Rim Light와 Fill Light

Rim Light
외각선을 강조하는 테크닉을 Rim Light라고 한다
카메라 벡터(C)・법선 벡터(N)가 0이거나 0에 근사한 값일 경우
(시선 벡터다, 광원 벡터가 아니다!!)
이는 가시성 판단에 의해서 외곽선이라고 할 수 있다
계산식은 1 - 시선 벡터・노멀 벡터
※1에서 빼는 이유
빛이 들어오는 것이 아니라 나간다고 생각해야 한다(계산이)
cosθ는 90도일 때 0(가장 어두움), 0도일 때 1(가장 밝음)
Rim Light는 1보다 작기 때문에 제곱하면 더 작아짐
적당히 제곱하고, 색을 입히고 기본 출력 값에 더하면 외곽선이 만들어진다
Fill Light
역광이지만 캐릭터에게 일정 정도의 밝기를 주고 싶을 때 사용한다
외곽선 부분이 어두워지기 때문에 상대적으로 캐릭터의 밝기가 부각된다
내적의 용도 - 방향 계산
캐릭터를 이동시키는 과정에 사용된다
- 2차원 스크린 화면의 위치를 3차원 공간상의 좌표로 변환하기
= 언프로젝션 - 캐릭터의 방향을 그 위치 방향으로 회전 시키기
- 디렉셔널 벡터(캐릭터의 방향), 현재 좌표, 이동할 좌표
- 이동할 좌표 - 현재 좌표 = 타겟 벡터
- 디렉셔널 벡터・(방향만 필요하기 때문에 정규화)타겟 벡터 = 코사인 세타의 값
(디렉셔널 벡터는 기본적으로 정규화 되어 있음) - 코사인의 값에서 각도를 구하는 것이 아크 코사인
- 디렉셔널 벡터(캐릭터의 방향), 현재 좌표, 이동할 좌표
- 캐릭터를 그 위치로 이동시키기

계산한 θ만큼 회전시키고 이동해야 한다
벡터 연산 - 외적
두 벡터를 외적하면 두 벡터의 직교(!)하는 벡터가 나온다
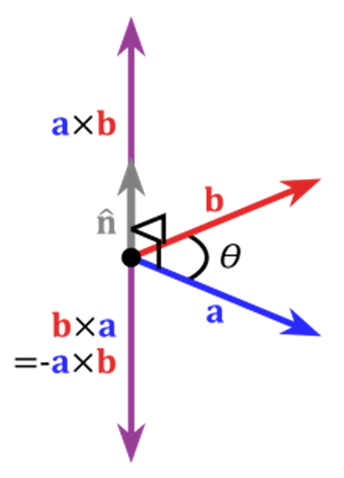
내적은 교환 법칙이 성립하지만 외적은 성립하지 않는다
직교하는 벡터는 2가지 방향이 있기 때문
오른손 법칙!!
카메라는 위가 어느 방향인지를 나타내는 벡터와,
캐릭터가 어디를 바라보고 있는지 나타내는 벡터(디렉셔널 벡터)는 항상 지니고 있다.
좌, 우로 움직일 때는??
위 방향 벡터와 디렉셔널 벡터를 외적하면 나온다
캐릭터 이동 시, 회전할 크기(각도)를 구했다고 하더라도
방향은 아직 모른다.
이때 벡터의 외적으로 왼쪽인지 오른쪽인지 알 수 있다
외적의 용도 - 면의 법선 벡터
점 3개가 있으면 3차원 공간상에 평면을 만들 수 있다
문제는 그렇게 만든 평면의 어디가 앞, 뒤인지 판단할 수 있을까?
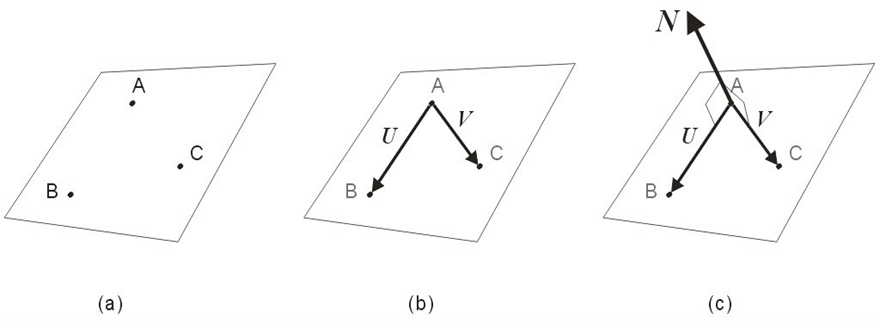
U = B - A
V = C - A
외적 U x V을 하면 법선 벡터 N를 구할 수 있다
여기서 외적의 순서를 바꾸어 외적 V x U을 하면 반대 방향을 앞면으로 설정할 수도 있다
또한 벡터는
총알이 날아가는 직선의 방정식,
외적을 이용해서 평면의 방정식,
충돌 여부를 확인해서 충돌(피탄) 좌표를 구하기
피탄 좌표가 삼각형에 포함되어 있는지 한 번 더 확인하기
등에도 사용된다
SSS
'게임 프로그래밍(학습 내용 정리) > 게임 수학' 카테고리의 다른 글
| 변환 파이프라인 (0) | 2022.01.04 |
|---|---|
| 좌표계 (0) | 2021.12.28 |
| 행렬 (0) | 2021.12.21 |
| 삼각비와 삼각 함수 (0) | 2021.11.09 |
| 수열(Sequence)과 급수(Series) (0) | 2021.10.26 |




