Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Rim Light
- VR
- 벡터
- ASW(Application SpaceWarp)
- Toon Shader
- Cartoon Rendering
- 게임 수학
- 메모리 누수
- 가상 바이트
- 작업 집합
- Windows Build
- ColorGradingLutPass
- 개인 바이트
- 3d
- working set
- Three(Two) Tone Shading
- Cell Shader
- C언어
- OculusMotionVectorPass
- URP
- Virtual Byte
- AppSW
- Private Bytes
- URP로 변경
- 프로그래밍 기초
- Cell Look
- Specular
Archives
- Today
- Total
WinCNT
좌표계 본문
직교 좌표계
일반적으로 알고 있는 평범한 좌표계
3D 그래픽스에서도 일반적으로 사용된다
원기둥 좌표계
충돌 처리할 때 많이 사용되는 좌표계
구면 좌표계
충돌 처리할 때 많이 사용되는 좌표계
직교 좌표계로 변환하는 식

오브젝트에 대해서는 공통된 좌표계를 써야 해야 한다
그래야 같은 공간에 오브젝트들을 같이 올릴 수 있다
3대 변환
이동, 회전, 크기
변환 – 이동(Translation)

변환 – 회전(Rotation)

변환 - 전치행렬
행렬의 기저벡터가 직교일 때 전치행렬 = 역행렬이므로 연산량을 줄일 수 있다
변환 적용
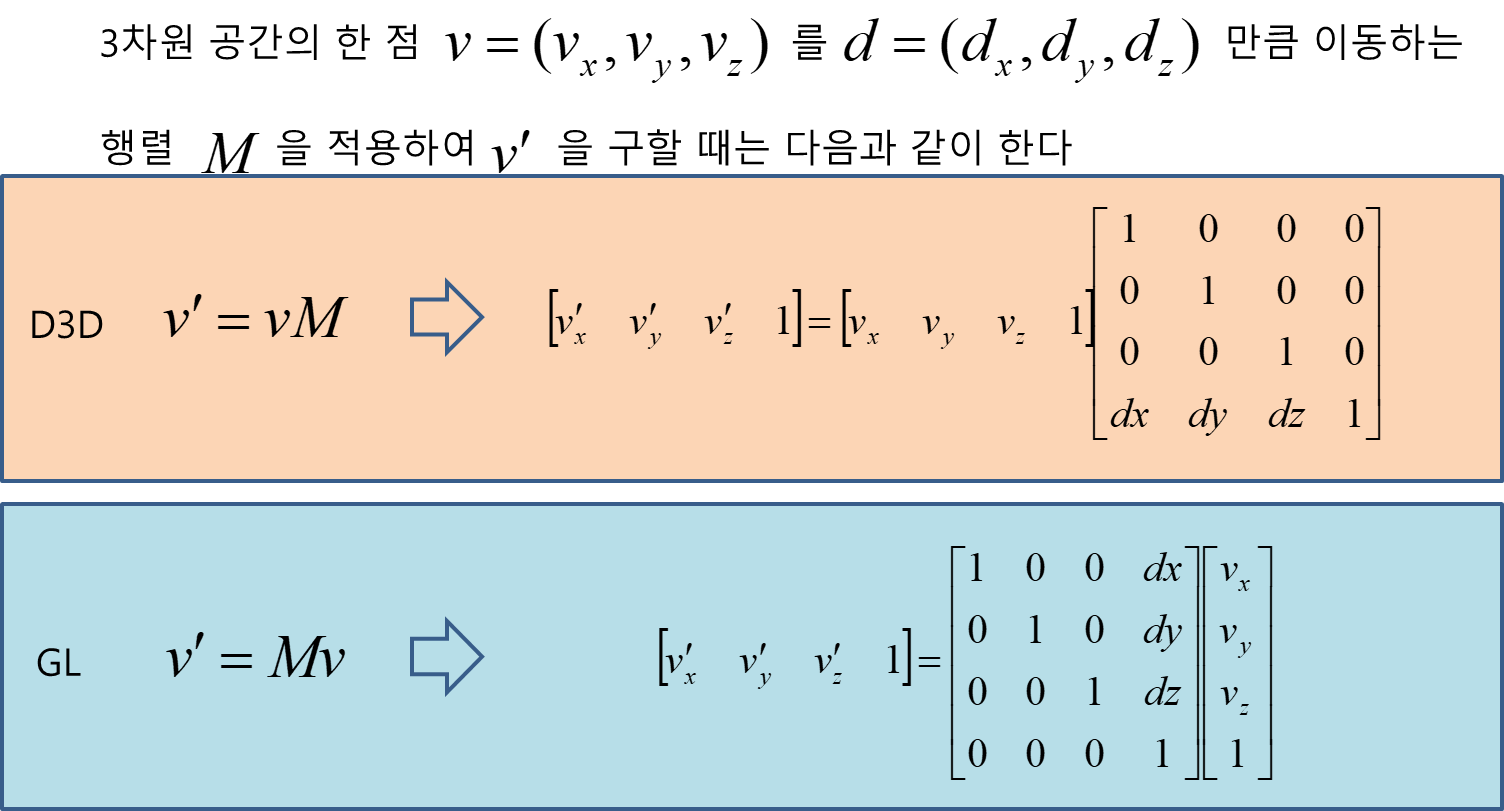
D3D 방식으로 계산하면 v'은 다음과 같다
변환 결합(concatenation)
행렬의 특징은 결합법칙이 성립한다는 것이다. 즉, 다음 두 수식은 동치다

회전 변환 - 오일러 변환
회전 변환에서 주로 사용하는 행렬

그 외에도 각축 방식, 쿼터니언 등등이 있다
(오일러 변환 방식과 쿼터니언은 서로 변환 가능함)
크기 변환

강체(rigid body), 비강체(sotf body)
변환이 일어나지 않는 것들 = 강체
관절이 있는 것들 = 비강체
- 기하학적 모양은 변경하지 않는 것이 강체(rigid body)변환
- 방향,위치만 변경(이동,회전)에 해당
- 기하학적 모양이 변경되는 것이 비강체 변환
- 크기변환이 이에 해당
모델링한 캐릭터에 아트팀이 뼈대를 심는다(리깅)
뼈대의 움직임에 따라 뼈대에 딸려 있는 스킨(폴리곤)도 같이 움직임
문제는 두 개 이상의 뼈대에 영향을 주거나 받는 경우가 있다는 것
(계층 구조도 겹치고 아무튼 문제가 많음)
하지만 기본적인 연산은 버텍스와 행렬 연산일 뿐이다
번외) 행렬에서의 T
Transpose 행렬 = 전치 행렬
Translation 행렬 = 이동 행렬
Transform 행렬 = 변환 행렬(이동, 회전, 크기 행렬을 모두 곱해둔 행렬)
헷갈리지 말자...
SSS
'게임 프로그래밍(학습 내용 정리) > 게임 수학' 카테고리의 다른 글
| 계층 구조와 애니메이션 보간 기초 (0) | 2022.01.11 |
|---|---|
| 변환 파이프라인 (0) | 2022.01.04 |
| 행렬 (0) | 2021.12.21 |
| 삼각비와 삼각 함수 (0) | 2021.11.09 |
| 수열(Sequence)과 급수(Series) (0) | 2021.10.26 |




