| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Rim Light
- Cell Look
- 프로그래밍 기초
- URP로 변경
- 메모리 누수
- 3d
- 개인 바이트
- OculusMotionVectorPass
- ColorGradingLutPass
- 게임 수학
- URP
- 가상 바이트
- Three(Two) Tone Shading
- VR
- working set
- Cartoon Rendering
- Windows Build
- C언어
- Virtual Byte
- Cell Shader
- ASW(Application SpaceWarp)
- Specular
- AppSW
- Private Bytes
- 작업 집합
- 벡터
- Toon Shader
- Today
- Total
WinCNT
탐색과 정렬 알고리즘 본문
탐색 알고리즘
Linear Search
- 배열의 시작 부터 나올 때까지 탐색
- 정렬할 필요가 없음
Binary Search
- 정렬된 배열의 중간 부터 비교
- 검색 반경을 반으로 나누어 반복
Quick Search
- 퀵 정렬의 응용 버전
탐색이기 때문에 전체 정렬이 아니라 부분 정렬
정렬 알고리즘
캐시의 히트율을 높히기 위해 주로 배열을 사용하는 정렬 알고리즘에는 다음이 있다.
추가적으로 메모리 버퍼를 사용하지 않은 정렬 알고리즘(In_Place)
Bubble Sort(버블 정렬)
두 인접한 원소를 검사하여 정렬하는 방법, 시간복잡도는 O(n^2) 비교, O(n^2) 교환
장점: 코드가 단순하여 자주 사용됨
단점: 상당히 느리다
Select Sort(선택 정렬)

처음부터 마지막까지 봐서 가장 작은 게 1번째, 2번째……해서 (n-1)번 반복하는 정렬이다
시간복잡도는 일괄적으로 O(n^2)이다
void selectionSort(int *list, const int n)
{
int i, j, indexMin, temp;
for (i = 0; i < n - 1; i++)
{
indexMin = i;
for (j = i + 1; j < n; j++)
{
if (list[j] < list[indexMin])
{
indexMin = j;
}
}
temp = list[indexMin];
list[indexMin] = list[i];
list[i] = temp;
}
}장점: 이해하기 쉬운 알고리즘이다, 메모리가 제한적인 경우에 성능 상의 이점이 있다
단점: 상당히 느리다
Insertion Sort(삽입 정렬)
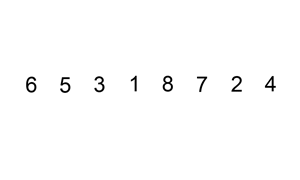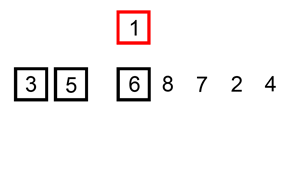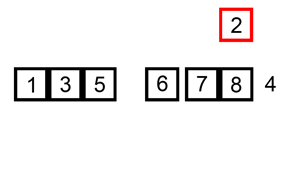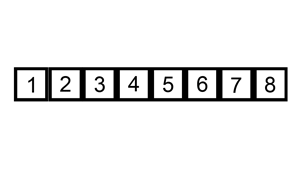
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여,
자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다
배열을 두 개 쓰거나, 한 칸씩 밀어내는 처리가 필요하다
시간복잡도는 최악의 경우 O(n^2)이다
장점 : 배열이 작을 경우에 상당히 효율적이다, 구현이 매우 쉽다
단점 : 자료를 한 칸씩 뒤로 밀어낼 때 오버헤드가 발생할 수 있다
Quick Sort(퀵 정렬)
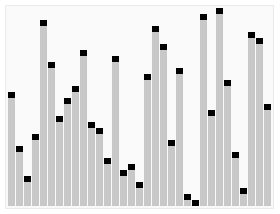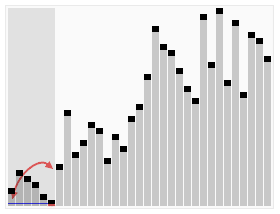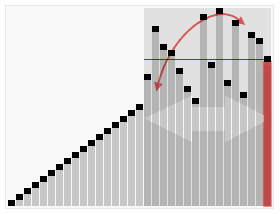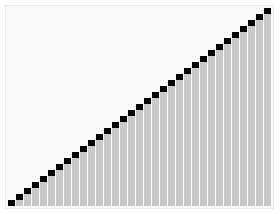
찰스 앤터니 리처드 호어가 개발한 정렬 알고리즘, 평균 시간복잡도는 O(n log n), 최악 시간복잡도는 O(n^2)
CPU의 캐시 히트율이 높도록 설계되어 있고, 매 단계에서 적어도 1개의 원소가 자기 자리를 찾게 되므로,
일반적인 경우 다른 정렬 알고리즘에 비해 훨씬 빠르게 동작한다.
(하지만 역정렬되어 있는 경우에는 얄짤없이 O(n^2)이다)
퀵 정렬에는 다음과 같은 특징이 있다
- 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬이다
- 중복한 값의 순서가 초기와 달라질 수 있는 불완전 정렬(Unstable Sort)이다
- 문제를 2개의 문제로 분리하고, 각각을 해결한 결과를 모아서 원래의 문제를 해결하는 분할 정복 알고리즘이다
퀵 정렬의 알고리즘의 과정은 다음과 같다
- 리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
- 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고,
피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다.
이렇게 리스트를 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
(이와 같이 어떠한 원소를 기준으로 나누는 작업을 파티션(partition)이라고 한다) - 분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다.
재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
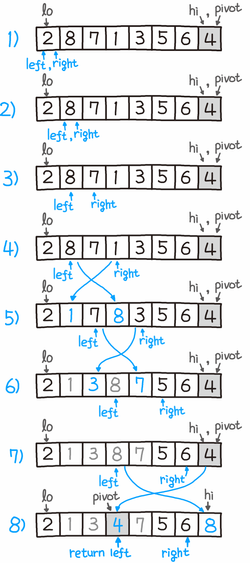
퀵 정렬의 가장 간단한 분할 알고리즘인 로무토 파티션의 도식은 다음과 같다.
(<파이썬 알고리즘 인터뷰> p.486, 책만, 2020)
피벗은 맨 오른쪽 값을 기준으로 하며, 이를 기준으로 2개의 포인터가 이동해서 오른쪽 포인터의 값이 피벗보다 작다면 서로 스왑하는 형태로 진행된다. 오른쪽 right 포인터가 이동하면서 피벗의 값이 오른쪽 값보다 더 클때, 왼쪽과 오른쪽의 스왑이 진행된다.
스왑 이후에는 왼쪽 left 포인터가 함께 이동 한다. 여기서 피벗의 값은 4이므로, 오른쪽 포인터가 끝에 도달하게 되면 4 미만인 값은 왼쪽으로, 4 이상인 값은 오른쪽에 위치하게 된다.
그리고 왼쪽 포인터의 위치로 피벗 아이템이 이동한다. 즉 그림에서 최종 결과인 8)을 보면, 4를 기준으로 작은 값은 왼쪽에, 큰 값은 오른쪽으로 분할되어 있고, 피벗이 그 중앙으로 이동하는 모습을 확인할 수 있다.
이렇게 계속 분할하면서 정복을 진행하여 코드 기준으로 left < right를 만족하지 않을 때까지, 즉 서로 위치가 역전할 때까지 계속 재귀로 반복되면서 정렬이 완료된다.
#include <algorithm>//swap
void quickSort(int A[], int low, int high) {
if(low >= high) return; // base condition
// divide process
int i = low, j = low;
int& pivot = A[high];
for (; j < high; ++j) {
if ( A[j] < pivot)
swap(A[i++], A[j]);
}
swap(A[i], pivot);
// conquer process
quickSort(A, low, i-1);
quickSort(A, i+1, high);
}
정렬을 위한 메모리 버퍼를 추가적으로 사용하는 정렬 알고리즘(Not In_Place)
Counting Sort(계수 정렬)
정수형, 분포가 크지 않은 데이터의 정렬에 적합한 알고리즘
대상의 요소에 대해서 버퍼(배열 등)에 그 개수를 카운팅하고
Radix Sort(기수 정렬)
십진법과 Counting Sort를 응용하는 알고리즘
처음에는 1의 자리의 숫자를 Counting Sort로 비교하고, 그 다음은 10의 자리의 숫자를 비교하는 식으로
가장 큰 자리의 숫자까지 반복하여 정렬하는 방식이다.
(십진법에서는 0~9까지의 숫자밖에 존재하지 않으므로 Counting Sort를 사용함)
Merge Sort(병합 정렬)
작은 버퍼로 대상의 요소들을 다 나눈 뒤, 다시 합치면서 정렬하는 알고리즘
이진 트리
Heap Sort(힙 정렬)
가장 빠른 정렬 알고리즘
Introsort(또는 Introspective 정렬)
기본적으로 퀵 정렬 + 힙 정렬로 구성된 하이브리드 정렬 알고리즘이다.
빠른 평균 성능과 최적화된 최악의 성능을 모두 제공한다(std의 Sort 알고리즘이 바로 Introsort)
Introsort의 평균, 최악 시간복잡도는 모두 O(n log n)를 가진다.
// Introsort의 슈도 코드
procedure sort(A : array):
let maxdepth = ⌊log2(length(A))⌋ × 2
introsort(A, maxdepth)
procedure introsort(A, maxdepth):
n ← length(A)
if n ≤ 1:
return // base case
else if maxdepth = 0:
heapsort(A)
else:
p ← partition(A) // assume this function does pivot selection, p is the final position of the pivot
introsort(A[0:p-1], maxdepth - 1)
introsort(A[p+1:n], maxdepth - 1)전체적인 흐름은 퀵 정렬과 같으나, 재귀 호출의 최대 깊이(maxdepth)를 설정해서,
그 깊이 이상으로 재귀 호출이 될 경우 O(n log n)이 보장되는 힙 정렬을 수행한다.
SSS
'게임 프로그래밍(학습 내용 정리) > 자료구조와 알고리즘' 카테고리의 다른 글
| 페이지 교체와 알고리즘 (0) | 2022.01.03 |
|---|---|
| B Tree와 Red-Black Tree (0) | 2021.12.27 |
| 힙 정렬(Heap Sort)과 B Tree (0) | 2021.12.21 |
| 트리(Tree)와 자료 구조의 힙(Heap) (0) | 2021.12.20 |
| 자료구조와 알고리즘 (0) | 2021.12.06 |



